Εκπαιδευτικοί-Δημόσιοι υπάλληλοι: Πώς διαμορφώνονται τα νέα εφάπαξ

Τα νέα εφάπαξ για το Δημόσιο, με βάση τις πληρωμές του πρώτου διμήνου του 2024, διαμορφώνονται ως εξής:

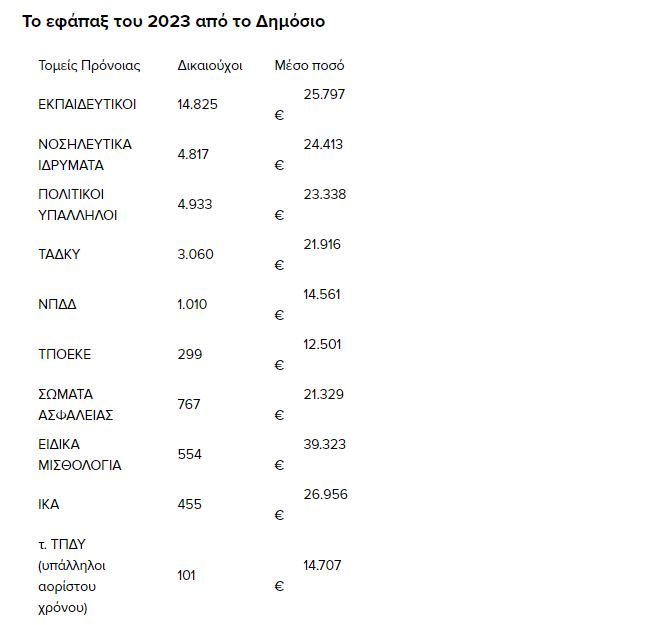
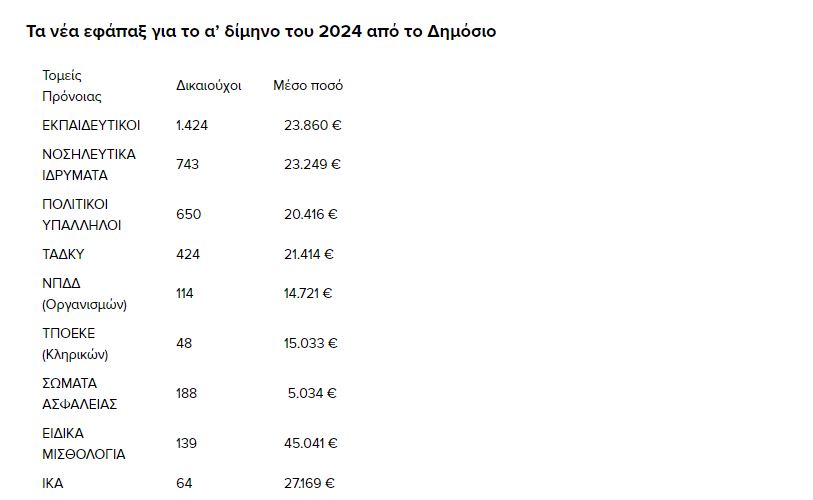
• Οι συνταξιούχοι εκπαιδευτικοί παίρνουν κατά μέσο όρο εφάπαξ 23.860 ευρώ (25.797 ευρώ μέσο εφάπαξ το 2023).
• Οι συνταξιούχοι από τα δημόσια νοσοκομεία (νοσηλευτικό, διοικητικό προσωπικό) παίρνουν κατά μέσο όρο εφάπαξ 20.416 ευρώ (24.413 ευρώ μέσο εφάπαξ το 2023).
• Οι συνταξιούχοι δημοτικοί υπάλληλοι πληρώνονται για τις αιτήσεις του 2024 κατά μέσο όρο εφάπαξ 21.414 ευρώ (21.916 ευρώ μέσο εφάπαξ το 2023).
• Οι συνταξιούχοι κληρικοί, που πλέον με διάταξη νόμου μπορούν να πάρουν το εφάπαξ από το 67ο έτος συνεχίζοντας το λειτούργημά τους, πληρώνονται κατά μέσο όρο εφάπαξ 15.033 ευρώ (12.501 ευρώ μέσο εφάπαξ το 2023).
• Οι συνταξιούχοι των ειδικών μισθολογίων παίρνουν κατά μέσο όρο εφάπαξ 45.041 ευρώ (39.323 ευρώ μέσο εφάπαξ το 2023).
• Οι συνταξιούχοι υπάλληλοι του ΙΚΑ παίρνουν κατά μέσο όρο εφάπαξ 27.169 ευρώ (26.956 ευρώ μέσο εφάπαξ το 2023).

Τι ισχύει για όσους αποχωρούν μετά το 2014
Ο κανόνας που εισήγαγε ο νόμος 4387/2016 είναι ότι το εφάπαξ για τα ίδια έτη ασφάλισης βαίνει μειούμενο κάθε χρόνο για όσους συνταξιοδοτούνται από 1ης/1/2014 και μετά.
Για να ισοφαρίσουν οι ασφαλισμένοι τις απώλειες, θα πρέπει να παραμείνουν περισσότερα χρόνια.
H εφημερίδα ” Ελεύθερος Τύπος παραθέτει παρακάτω σχετικά παραδείγματα:

• Υπάλληλος που συνταξιοδοτήθηκε από το Δημόσιο το 2013 με 37 έτη και μισθό 1.600 ευρώ πήρε εφάπαξ 35.520 ευρώ, ενώ ένας υπάλληλος που αποχώρησε το 2022 με 37ετία και τον ίδιο περίπου μισθό πήρε εφάπαξ 27.372 ευρώ.
• Υπάλληλος που θα συνταξιοδοτηθεί το 2024 από το Δημόσιο με 37 έτη και μέσο μισθό 1.600 ευρώ θα πάρει εφάπαξ 26.500 ευρώ, ενώ ένας υπάλληλος που θα βγει στη σύνταξη το 2029, έχοντας τότε 37ετία και τον ίδιο περίπου μισθό, θα πάρει εφάπαξ 21.740 ευρώ.

Η μείωση που προκαλεί ο νόμος Κατρούγκαλου με την άτοκη επιστροφή εισφορών στο εφάπαξ είναι σχεδόν 10.000 ευρώ σε μία 10ετία (2023 έναντι 2013) και όσο αυξάνονται τα έτη με τις άτοκες επιστροφές από το 2014 και μετά οι απώλειες θα μεγαλώνουν.
Πώς θα διαμορφωθεί το εφάπαξ του Δημοσίου στα επόμενα χρόνια
Με το ισχύον σύστημα που θεσπίστηκε με το νόμο 4387/2016 (νόμος Κατρούγκαλου), το εφάπαξ σε όλα τα Ταμεία (πλην των στρατιωτικών) υπολογίζεται με δύο τρόπους ως εξής: 

• Το πρώτο τμήμα του εφάπαξ αντιστοιχεί στα έτη ασφάλισης ως το 2013 και για το διάστημα αυτό το ποσό υπολογίζεται με το 60% του μέσου όρου των αποδοχών των ασφαλισμένων για την 5ετία 2009-2013.
• Το δεύτερο τμήμα του εφάπαξ αντιστοιχεί στα έτη ασφάλισης από το 2014 μέχρι τη συνταξιοδότηση των ασφαλισμένων και ισοδυναμεί με την επιστροφή των εισφορών που καταβάλλουν μετά το 2024.

Το διπλό σύστημα υπολογισμού ευνοεί τους παλαιότερους ασφαλισμένους που είναι πιο κοντά στην «καλή» 5ετία του εφάπαξ (2009-2013).
Η εφημερίδα “Ελεύθερος Τύπος παραθέτει παρακάτω σχετικά παραδείγματα:

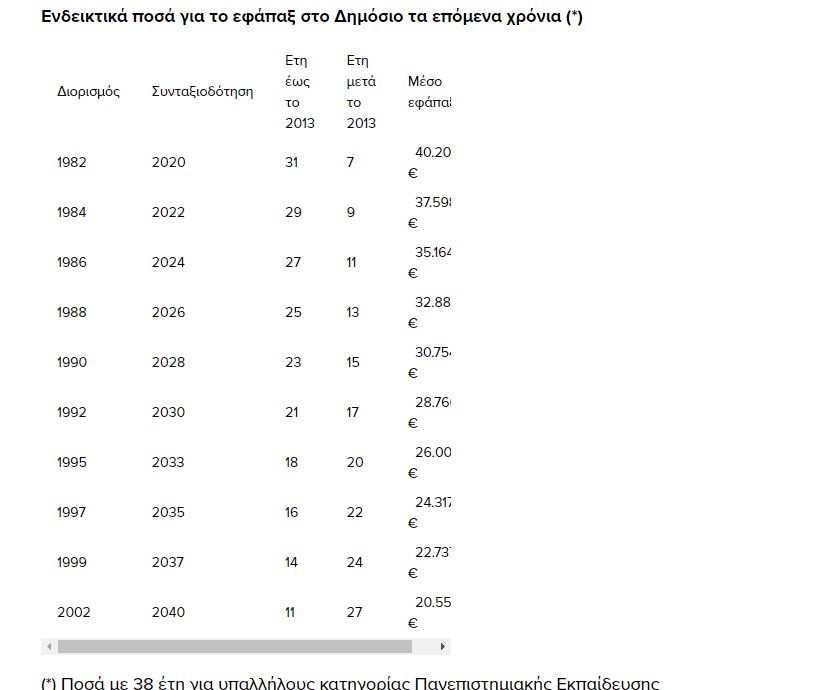
• Δημόσιος υπάλληλος με 38 έτη, που συνταξιοδοτήθηκε το 2020 και είχε μέσο μισθό 1.800 ευρώ στην 5ετία 2009-2013 και 2.000 ευρώ από το 2014 ως το 2020, πήρε εφάπαξ 40.200 ευρώ (33.480 ευρώ για την 5ετία 2009-2013 και 6.720 ευρώ για την 7ετία 2014-2020).
• Δημόσιος υπάλληλος που θα συνταξιοδοτηθεί με 38 έτη το 2024 θα πάρει εφάπαξ περίπου στις 35.160 ευρώ, γιατί θα έχει λιγότερα έτη ως το 2013 και μικρότερο μέσο όρο αποδοχών μεταξύ 2009-2013, οπότε το «καλό τμήμα» του εφάπαξ θα βγει μικρότερο. Σε σύγκριση με τον ασφαλισμένο που αποχώρησε το 2020, ο συνταξιούχος του 2024 έχει χάσει περίπου 5.000 ευρώ.
• Δημόσιος υπάλληλος που θα συνταξιοδοτηθεί με 38 έτη το 2030 θα πάρει εφάπαξ περίπου στις 28.760 ευρώ, γιατί θα έχει λιγότερα έτη ως το 2013 και μικρότερο μέσο όρο αποδοχών μεταξύ 2009-2013, οπότε για αυτό το διάστημα θα πάρει μικρότερο εφάπαξ. Σε σύγκριση με τον ασφαλισμένο που αποχώρησε το 2020, ο συνταξιούχος του 2030 θα έχει χάσει περίπου 11.500 ευρώ και σε σχέση με τον συνταξιούχο του 2024 θα πάρει 6.400 ευρώ λιγότερα